Salem Nkunda Nyisingize

RNN pour la prévision de séries temporelles

Deep Learning · Séries temporelles · Lecture ~15 min

1) Introduction

Les séries temporelles sont des données séquentielles : l’ordre compte, et le passé influence le futur. Les modèles classiques (par exemple AR) rendent cette dépendance explicite via des retards (lags) fixes. Les réseaux de neurones, eux, ont besoin d’un mécanisme interne pour « transporter » l’information à travers le temps.

Les Recurrent Neural Networks (RNN) répondent précisément à ce besoin en introduisant un état interne.

C’est pour cela qu’on dit qu’un réseau est “récurrent”.
À mesure qu’une nouvelle valeur de la séquence arrive, le réseau recalcule son état caché en combinant l’entrée courante avec l’information accumulée aux pas précédents.

Ce principe est commun à toutes les architectures récurrentes : RNN, GRU et LSTM.
RNN déroulé dans le temps montrant la mise à jour de l’état caché
RNN déroulé (unrolled) : à chaque pas de temps, l’état caché est mis à jour et transmis au pas suivant.

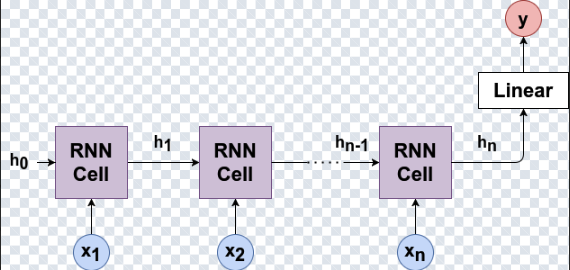
2) RNN et prévision : une lecture “auto-régressive”

Dans une perspective séries temporelles, on peut voir un RNN comme un modèle auto-régressif non linéaire dont la mémoire est apprise.

Idée AR classique :

x_{t+1} = f(x_t, x_{t-1}, ..., x_{t-p})

Un RNN remplace l’ordre fixe p par un état caché qui résume l’historique : 

h_t = f(h_{t-1}, x_t)
x̂_{t+1} = g(h_t)

L’état caché agit comme une compression adaptative du passé : le modèle apprend automatiquement combien d’historique est utile.

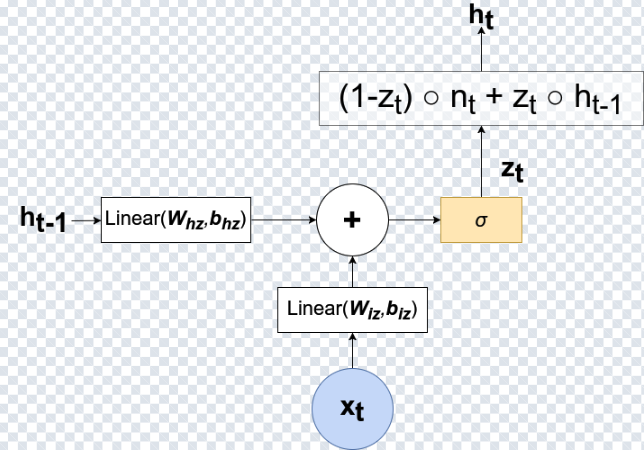
GRU update gate and hidden state update mechanism
Mécanisme GRU : z_t combine l’état caché précédent et l’état candidat pour produire h_t.

Limite des RNN conventionnels : gradients qui s’éteignent

Sur des séquences longues, les RNN conventionnels ont du mal à apprendre des dépendances lointaines (problème des vanishing gradients). C’est exactement ce qui a motivé les architectures à portes : GRU et LSTM.

3) GRU : mémoire sélective, plus simple que LSTM

Les Gated Recurrent Units (GRU) atténuent le problème des gradients en introduisant des portes (gates) qui contrôlent la conservation et l’oubli de l’information. Un GRU utilise deux portes :

  • Reset gate : contrôle ce qu’on “oublie” du passé.
  • Update gate : contrôle ce qu’on garde du passé vs ce qu’on remplace par de la nouvelle info.

Le cœur du GRU est une interpolation douce entre l’ancien état et un état candidat : 

h_t = (1 - z_t) ⊙ h_{t-1} + z_t ⊙ h̃_t

Cette idée (préserver ou mettre à jour) rend l’apprentissage plus stable et souvent plus rapide qu’avec LSTM, tout en gardant d’excellentes performances en prévision.

Unrolled RNN over time showing hidden state updates across timesteps
RNN déroulé : l’état caché se met à jour pas à pas au fil des entrées.

4) Insight mathématique (compact)

Voici une version compacte des équations (utile si vous voulez relier intuition et formalisme).

GRU (résumé)

z_t = σ(W_z x_t + U_z h_{t-1} + b_z)
r_t = σ(W_r x_t + U_r h_{t-1} + b_r)
h̃_t = tanh(W_h x_t + U_h (r_t ⊙ h_{t-1}) + b_h)
h_t = (1 - z_t) ⊙ h_{t-1} + z_t ⊙ h̃_t

Intuition : l’update gate empêche d’écraser inutilement une bonne mémoire — ce qui aide pour les dépendances plus longues.

5) LSTM : mémoire explicite via l’état de cellule

Les LSTM introduisent un état supplémentaire ct (cell state) qui agit comme une “autoroute” de mémoire à long terme. Cette structure donne un contrôle plus fin sur la conservation et la sortie d’information, au prix d’une complexité et d’un coût de calcul plus élevés.

Trois portes régulent la mémoire :

  • Forget gate : ce qu’on supprime.
  • Input gate : ce qu’on écrit.
  • Output gate : ce qu’on expose via l’état caché.
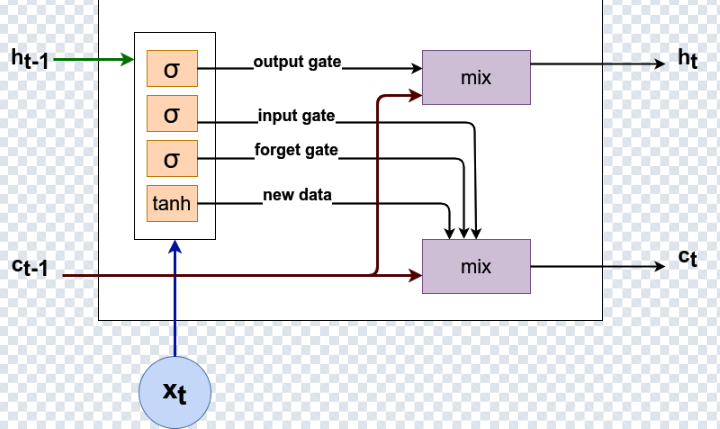
LSTM cell with forget, input, and output gates controlling the cell state and hidden state
Cellule LSTM : les portes contrôlent l’état de cellule c_t (mémoire long terme) et l’état caché h_t (sortie exposée).

Équations compactes (LSTM)

f_t = σ(W_f x_t + U_f h_{t-1} + b_f)
i_t = σ(W_i x_t + U_i h_{t-1} + b_i)
o_t = σ(W_o x_t + U_o h_{t-1} + b_o)
c_t = f_t ⊙ c_{t-1} + i_t ⊙ c̃_t
h_t = o_t ⊙ tanh(c_t)

En pratique : LSTM peut être meilleur sur des horizons très longs (saisonnalité, tendances longues, changements structurels), mais GRU est souvent un excellent compromis.

6) Comparaison rapide (prévision)

Modèle Mémoire Complexité Meilleur cas
RNN État caché uniquement Faible Séquences courtes
GRU État caché + portes Moyenne Prévision générale (bon défaut)
LSTM État caché + état de cellule Élevée Dépendances très longues

Règle pratique : commencez par un GRU. Passez au LSTM si vous avez réellement besoin d’une mémoire très longue.

7) Conclusion

Les architectures récurrentes offrent une base naturelle pour la prévision en séries temporelles : elles mettent en œuvre une récurrence d’état qui transporte le passé dans le présent. Les RNN conventionnels sont limités sur les longues séquences, ce qui justifie l’intérêt des GRU et des LSTM.

Les GRU donnent souvent un excellent compromis entre stabilité, performance et coût de calcul. Les LSTM restent très pertinents quand la dépendance long terme est déterminante.

Références